Reversible Instance Normalization for Accurate Time-Series Forecasting Against Distribution Shift - 论文阅读

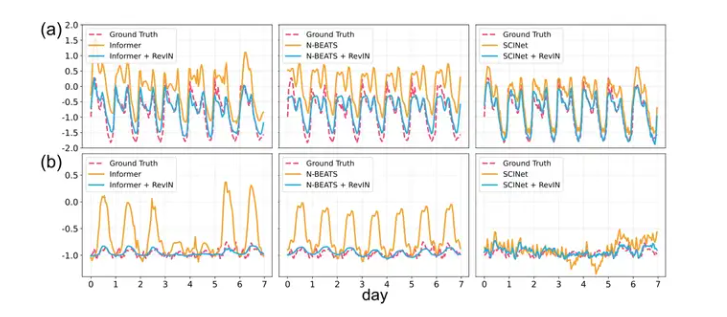
时间序列中的统计属性经常发生变化，即数据分布随时间而变化。这种时间分布变化是阻碍准确时间序列预测的主要挑战之一。为了解决这个问题，我们提出了一种简单但有效的归一化方法，称为可逆实例归一化（RevIN）。具体来说，RevIN 由两个不同的步骤组成，归一化和非归一化。前者对输入进行归一化以根据均值和方差来固定其分布，而后者将输出返回到原始分布。此外，RevIN 与模型无关，通常适用于各种时间序列预测模型，预测性能有显着提高。如图 1 所示，RevIN 有效地增强了基线的性能。我们广泛的实验结果验证了对各种现实世界数据集的普遍适用性和性能改进。

前言

文章中认为，时序预测模型具有和其它DNN一样的性质，即对于数据输入的分布敏感。几乎所有的DNN，都是在尝试从某个数据分布中找出与之对应的值或分布，因此BN，LN这种归一化层能够让训练效果变得更好（个人以为是更容易使模型收敛）。

时序中输入分布问题在于，每一个时间戳的输入，都和上下文有关系，但是又可以看作和上下文的分布都不同，文章中采用偏移的说法。目前的Informer，N-Beats等都没有做这方面的工作，因此文章在研究后提出了RevIN：可逆实例归一化，用来在时序数据上平稳输入的分布。

Proposed Method

• 首先设置一些变量，后面用：
• Tx ：输入数据的滑动窗口大小
• N ：序列数量
• K ：变量数-
• Ty ：预测长度

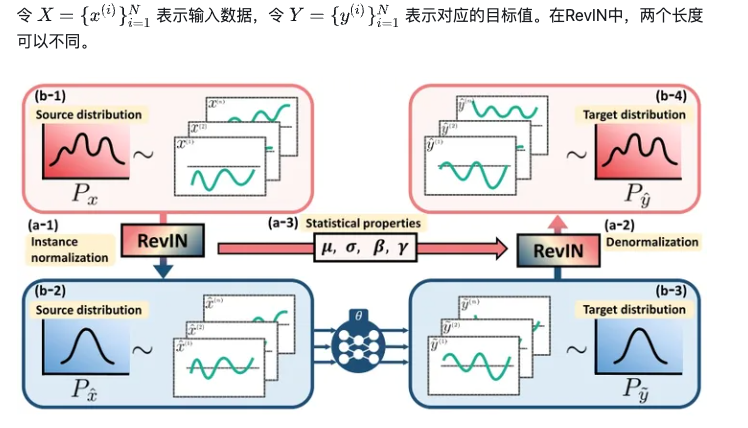
上图描述了一个基本的work flow：输入一个向量x，即它实际上可以看作一个多变量，每一个维度可以看作一个单变量。x通过RevIN，将b-1的分布转换到b-2，可以看到它的均值发生了改变，每一个单变量都针对均值做了归一化，这样原始分布中不同单变量之间的分布差异被人为的减少。将变换分布后的x_hat当作输入给网络，输出y_tilde（不想打tex了，知道是哪个就行），这些y_tilde具有b-3的分布，但也许不符合真实的分布。所以a-1的RevIN中间有一些参数，其中代表均值和方差就不提了，β是进行归一化的参数，γ是进行仿射变换的可学习参数。通过这些参数，b-3通过RevIN做一次reversing，回归近似真实的分布b-4。

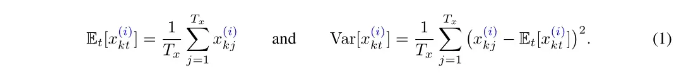
其中均值和方差的计算（1）已给出。而具体的归一化公式（2）也给出，减均值除标准差后乘γ加上β。减去均值除标准差就是典型的变成高斯分布，γ个人理解是决定了高斯峰值，β决定了偏移方向。这种归一化操作其实并不少见，autoformer里也用到均值等去查看趋势性。

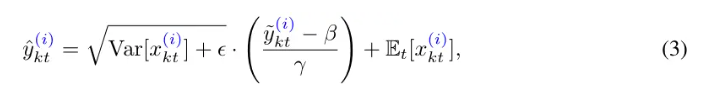
通过反转归一化，获得与输入同分布的预测值。这里的操作就是对归一化的操作取倒数。

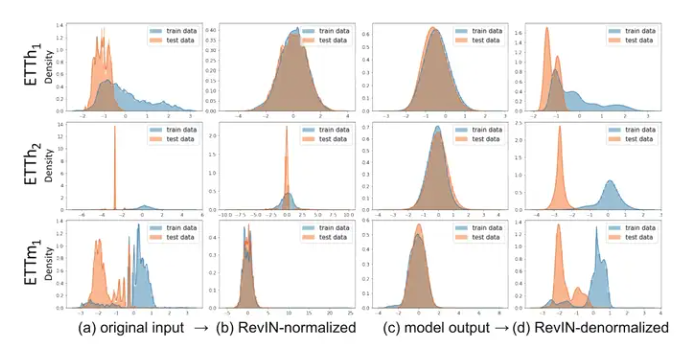
Figure3清楚展示了整个work flow中数据的分布变化。可以看到在分布不算太尖锐时，RevIN的归一化效果是还不错的，逆归一化时，大致的趋势相同，但是小范围的波动误差仍然广泛存在。而对于尖锐的分布，逆掉以后可以发现输出分布变平稳了，很难说这是不是好的现象。因为其与原始分布的误差已经比较明显的体现，但是在未知数据集中这种更为平稳的输出分布可能会有更好的泛化性能。（信一手大数定律。

论文里提到这种过网络之前先过RevIN的结构相比传统的BN使用，更像是Encoder-Decoder，将RevIN解读维编码器/解码器也许会更好。这种层的作用并不是直接解决层间更新参数分布的偏移问题，而是有点像传统机器学习中的归一化，先清洗数据，最后反回来求。

即RevIN是一种模型无关的方法。

Experiments Results

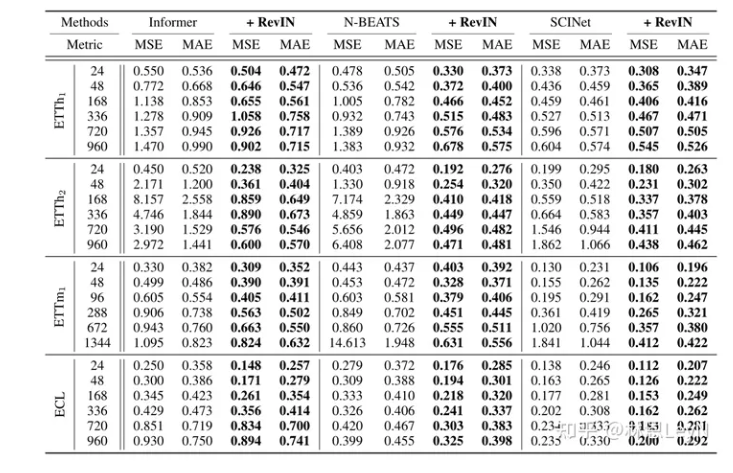
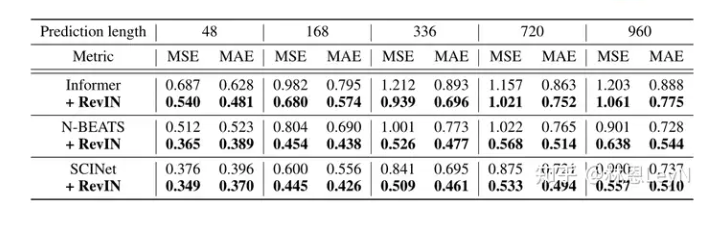
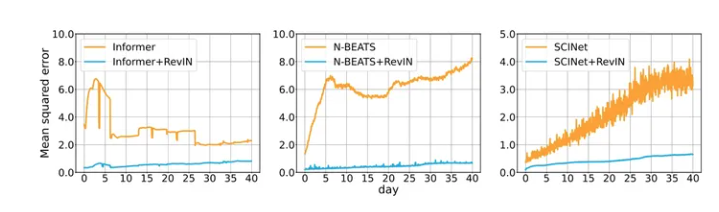
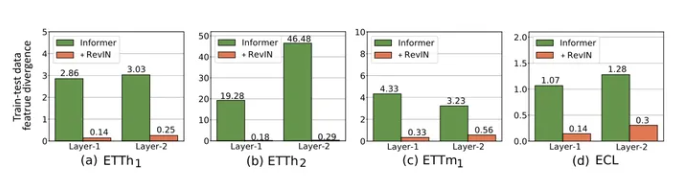
结果很清晰，加了RevIN的模型，鲁棒性upup。

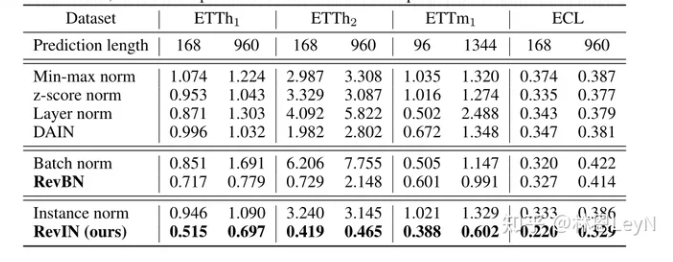
文中还提到了RevIN与其他一些归一化方法的比较。 将 RevIN 与经典和最先进的归一化方法进行比较，包括 minmax 、z-score、LN、BN、实例归一化和深度自适应输入归一化 (DAIN)。针对每个输入实例计算 min-max 和 z-score 归一化方法的归一化统计数据，而不是对于整个数据。此外，我们使用BN来替代 RevIN 中的输入归一化方法，称为RevBN。

这里只提一下RevBN，Rev操作极大的提升了BN的预测性能，但是因为BN是从所有数据中作归一化，所以很难分别输入和输出之间的分布差异。因此实际实验RevIN效果更好些。同时RevIN在参数量方面大获全胜。

Discussion

后面Appendix部分的附加实验很多，效果无一例外的都在显示RevIN的实用性。而说到底，这也是一个inspiration类型的工作，不过A+B加的是归一化的思想，而不是具体方法。读论文时还在进行双盲审稿，不知道现在结果怎么样。可逆实例归一化（Reversible Instance Normalization）在时间序列预测中的应用，旨在提高模型在面对分布变化时的准确性。通过引入可逆性，研究者希望在保留重要特征的同时，减少信息损失，从而提升模型的鲁棒性和预测性能。它能有效应对分布变化带来的挑战。通过可逆归一化，模型不仅保留了原始数据的关键信息，还增强了对不同数据分布的适应能力，从而提高预测的准确性和稳定性。这种灵活性特别适合时间序列数据的动态特性。